integral odd function|Odd Function : Baguio Sometimes we can simplify a definite integral if we recognize that the function we’re integrating is an even function or an odd function. If the function is neither even nor odd, then we proceed with integration like normal. The De La Salle John Bosco College (DLSJBC) is a PAASCU-accredited Lasallian district school located in Mangagoy, Bislig, Surigao del Sur in the Philippines.
PH0 · integrals of even and odd functions
PH1 · Odd Function
PH2 · Integrating Even and Odd Functions
PH3 · Integrals of even/odd functions — Photomath
PH4 · Definite integrals of even and odd functions
PH5 · Definite integral of an odd function is 0 (symmetric interval)
PH6 · Definite integral of an odd function (KristaKingMath)
PH7 · Definite Integral of Odd Function
PH8 · 5.5: Indefinite Integrals and the Substitution Rule
PH9 · 5.4 Integration Formulas and the Net Change Theorem
Yes, Tajimaya Charcoal Grill Baguio City 2600 is taking precautions against COVID-19. A full list is available within the "safety precautions" section of this page. How is Tajimaya Charcoal Grill Baguio City 2600 rated?
integral odd function*******Definite integral of an odd function (KristaKingMath
Definite integrals of even and odd functions - Krista King MathIntegrating Even and Odd Functions | Calculus I - Lumen Learning
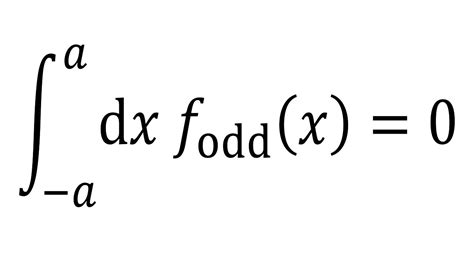
Integrals of even/odd functions — Photomath
Sometimes we can simplify a definite integral if we recognize that the function we’re integrating is an even function or an odd function. If the function is neither even nor odd, then we proceed with integration like normal.
But let’s start by remembering that limits can be defined as the restrictions on the .
Apply the integrals of odd and even functions. We saw in Module 1: Functions and Graphs that an even function is a function in which [Math Processing Error] f ( − x) = f ( x) for all [Math .integral odd function Odd Function If the range of the definite integral is -a to a, and if the function is odd, then the value of the integral is 0. To determine if the function is odd, plug -x in for x, and then simplify.
How to solve integrals of even/odd functions. Let’s see some integrals of even and odd functions in action! We’ll go through a few examples together. Example 1. Find the integral: ∫ − π π sin ( .Odd Function Examples of odd functions include x, x^3, the sine sinx, hyperbolic sine sinhx, tangent tanx, hyperbolic tangent tanhx, error function erf erf (x), inverse erf erf^ (-1) (x), and .integral odd functionA definite integral is either a number (when the limits of integration are constants) or a single function (when one or both of the limits of integration are variables). An indefinite integral represents a family of functions, all of which differ by a . Definite Integral of Odd Function - ProofWiki. Contents. 1 Theorem. 1.1 Corollary. 2 Proof. 3 Also see. 4 Sources. Theorem. Let f f be an odd function with a primitive on the open .
integrals of even and odd functions. Proof. Since the definite integral is additive with respect to the interval of integration, one has. Making in the first addend the substitution t= −x, dt=−dx t = .
Recall the integration formulas given in the table in Antiderivatives and the rule on properties of definite integrals. Let’s look at a few examples of .
For an odd function, I know that f (x) = - f (x). I'm trying to show that ∫a −a f(x)dx ∫ − a a f ( x) d x = 0. I've seen the proof where it splits the integral up into: ∫a 0 f(x)dx +∫0 −a . So, simple question; why does WolframAlpha fail to evaluate infinite bounded definite integrals of odd functions, stating that the solution "does not converge"? Is it not exactly accurate to say that the answer is zero? Edit: Rather, I should say that the integral over symmetric bounds, in general, of an odd function is zero. Why when we use .The product of any two odd functions is an even function. The quotient of any 2 odd functions is an even function. Composition: The composition of any 2 odd functions is odd. The derivative of any given odd function is even in nature. The integral of any given odd function from the limits – A to + A is 0. Similarly, if an even function is differentiable, then its derivative is an odd function while the integral of such a function over a symmetric interval is twice the value of its integral over the interval . Ostensibly, one can define a similar notion for multivariate functions by saying that such a function is odd if and only if As noted above we simply can’t integrate functions that aren’t continuous in the interval of integration. Also, even if the function was continuous at \(x = 1\) we would still have the problem that the function is actually two different equations depending where we are in the interval of integration. . Even and Odd Functions. This is the .
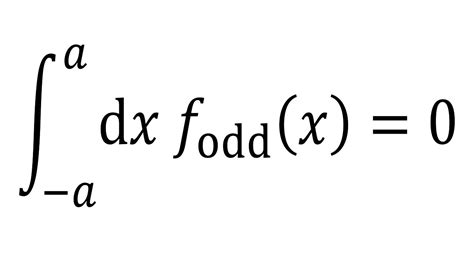
They are special types of functions. Even Functions. A function is "even" when: f(x) = f(−x) for all x In other words there is symmetry about the y-axis (like a reflection):. This is the curve f(x) = x 2 +1. They are called "even" functions because the functions x 2, x 4, x 6, x 8, etc behave like that, but there are other functions that behave like that too, such as cos(x):
5.4.4 Apply the integrals of odd and even functions. In this section, we use some basic integration formulas studied previously to solve some key applied problems. It is important to note that these formulas are presented in terms of indefinite integrals. Although definite and indefinite integrals are closely related, there are some key .
Many challenging integration problems can be solved surprisingly quickly by simply knowing the right technique to apply. While finding the right technique can be a matter of ingenuity, there are a dozen or so techniques that permit a more comprehensive approach to solving definite integrals. Manipulations of definite integrals may rely upon specific limits for the integral, like with odd .Several common types of functions have graphs that are symetric with respect to the y-axis or the origin, as shown in the next Figures. If the graph of y = f(x) is symmetric with respect to the y-axis, then we call f an even function. Similarly, if the graph of y = f(x) is symmetric with the respect to the origin, then we call f an odd function. Functions involving trigonometric functions are useful as they are good at describing periodic behavior. . requiring the power--reducing formula again. The \(\cos^3(2x)\) term is a cosine function with an odd power, requiring a substitution as done before. We integrate each in turn below. . Figure \(\PageIndex{2}\): Setting up Integration . The integration was not difficult, and one could easily evaluate the indefinite integral by letting \(u=\sin x\) or by letting \(u = \cos x\). This integral is easy since the power of both sine and cosine is 1. We generalize this integral and consider integrals of the form \(\int \sin^mx\cos^nx\ dx\), where \(m,n\) are nonnegative integers. In this video, we are finding the value of a definite integral of an odd function x^4 sin(x), with limits opposite of each other. Since the function is odd, .
average value of a function (or \(f_{ave})\) the average value of a function on an interval can be found by calculating the definite integral of the function and dividing that value by the length of the interval definite integral a .$\begingroup$ Is it given that the function is odd and thus you prove that the integral is zero, or is it given that the integral is zero and thus the function is odd? That's not clear. It seems like the second, but then the trouble starts with your second . In one of our classes the teaching assistant argued that $\int_\mathbb{R}ye^{-\frac{y^2}{2}}$ is an odd function and hence the integral is $0$. But this argument doesn't hold in the case of $\int x \frac{1}{1+x^2}$. In general when dealing with indefinite integrals I'm not allowed to use the argument odd-function, right?. I have to compute it . Even Odd Functions - Integration C5 S5 v3. Even Odd Functions - Integration C5 S5 v3. In this video I go over the theorem on integrating symmetric functions which greatly simplifies integration. For even functions the integral from -a to a is .
More integration tutorials:Integration with substitution: https://youtu.be/rv6LpW-YDyoPartial Integration: https://youtu.be/9517JtKv630Integration with t-for.
$\begingroup$ Since $\sin(x)$ is an odd function, with period $2\pi$, it's integral over any interval of length $2\pi$ is zero. As for the other two terms, can you show what you've tried so far? $\endgroup$ –
kamangyan accidentally upload video issue 🥺 pakireport po Kung sino nagsishare 🥺 #stopsharingthevideo #fyp #stopspreading #randomcontent . uranophile69.
integral odd function|Odd Function